复合变换

变换有三种状态：平移、旋转、缩放。

在一个四维矩阵中，是可以包含所有的变换状态的。即，我们可以让图形进行一次性的平移、旋转和缩放，这样的变换就叫做复合变换。

知识点

1. 矩阵乘法
2. 不同变换顺序的差异

第一章 矩阵相乘

矩阵相乘可以实现复合变换，就比如先位移再旋转、先旋转在位移，或着连续位移。

矩阵乘以矩阵的结果还是矩阵

1.使用 three.js 的 Matrix4 对象建立矩阵

const a = new Matrix4().set(
  0,
  1,
  2,
  3,
  4,
  5,
  6,
  7,
  8,
  9,
  10,
  11,
  12,
  13,
  14,
  15
);
const b = new Matrix4().set(
  0,
  10,
  20,
  30,
  40,
  50,
  60,
  70,
  80,
  90,
  100,
  110,
  120,
  130,
  140,
  150
);

注：set()方法里输入的矩阵是行主序的，但 elements 输出的矩阵是列主序的。

const ca = a.elements;
console.log(ca);

[0, 4, 8, 12, 1, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 15];

const cb = b.elements;
console.log(cb);

[0, 40, 80, 120, 10, 50, 90, 130, 20, 60, 100, 140, 30, 70, 110, 150];

2.让矩阵 a 乘以矩阵 b

const c = a.multiply(b);
console.log(c.elements);

[
  560,
  1520,
  2480,
  3440,
  620,
  1740,
  2860,
  3980,
  680,
  1960,
  3240,
  4520,
  740,
  2180,
  3620,
  5060,
];

分析一下结果

560=0*0 +1*40+2*80 +3*120
620=0*10+1*50+2*90 +3*130
680=0*20+1*60+2*100+3*140
740=0*30+1*70+2*110+3*150

1520=4*0 +5*40+6*80 +7*120
1740=4*10+5*50+6*90 +7*130
……

a 乘以矩阵 b 规律，以列主序的 ca、cb 为例：

先遍历 ca 的每一列，再遍历 cb 的每一行，将 ca 的每一列乘以 cb 的每一行，按照列主序排列后得到的结果。

列 --> 行 --> 列

或者，先遍历 ca 的每一行，再遍历 cb 的每一列，将 ca 的每一行乘以 cb 的每一列，按照行主序排列后得到的结果。

行 --> 列 --> 行

验证一下后者：

const cc = [];
for (let y = 0; y < 16; y += 4) {
  const [ax, ay, az, aw] = [ca[y], ca[y + 1], ca[y + 2], ca[y + 3]];
  for (let x = 0; x < 4; x++) {
    console.log(x);
    const [bx, by, bz, bw] = [cb[x], cb[x + 4], cb[x + 8], cb[x + 12]];
    cc.push(ax * bx + ay * by + az * bz + aw * bw);
  }
}
console.log(cc);

[
  560,
  1520,
  2480,
  3440,
  620,
  1740,
  2860,
  3980,
  680,
  1960,
  3240,
  4520,
  740,
  2180,
  3620,
  5060,
];

其结果和矩阵库一致。

3.通过上面的规则可知

• 当两个矩阵的每个元素相互等比时

a*b=b*a

• 当两个矩阵的每个元素相互不等比时

a*b!=b*a

第二章 复合变换的规律

1-位移加位移

物体沿 x 轴位移 ax，沿 y 轴位移 ay 后，再沿 x 轴位移 bx，沿 y 轴位移 by。

已知：

• 初始点位 A(ax,ay,az,1.0)
• 初次位移：沿 x 轴位移 bx，沿 y 轴位移 by
• 第二次位移：沿 x 轴位移 cx，沿 y 轴位移 cy

求：变换后的位置 F(fx,fy,fz,fw)

解：

1.设初次变换矩阵为 bm(行主序)：

[1.0, 0.0, 0.0, bx, 0.0, 1.0, 0.0, by, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0];

则初次变换后的点 F 为：

F = bm * A;
fx = (1.0, 0.0, 0.0, bx) * (ax, ay, az, 1.0) = ax + bx;
fy = (0.0, 1.0, 0.0, by) * (ax, ay, az, 1.0) = ay + by;
fz = (0.0, 0.0, 1.0, 0.0) * (ax, ay, az, 1.0) = az;
fw = (0.0, 0.0, 0.0, 1.0) * (ax, ay, az, 1.0) = 1.0;

2.设第二次变换矩阵为 cm(行主序)：

[1.0, 0.0, 0.0, cx, 0.0, 1.0, 0.0, cy, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0];

则第二次变换后的点 F 为第二次变换矩阵乘以上一次变换后的点 F：

F = cm * F;
fx = (1.0, 0.0, 0.0, cx) * (fx, fy, fz, 1.0) = fx + cx;
fy = (0.0, 1.0, 0.0, cy) * (fx, fy, fz, 1.0) = fy + cy;
fz = (0.0, 0.0, 1.0, 0.0) * (fx, fy, fz, 1.0) = fz;
fw = (0.0, 0.0, 0.0, 1.0) * (fx, fy, fz, 1.0) = 1.0;

通过第一次的变换，我们也可以这么理解最终的点 F：

fx = ax + bx + cx;
fy = ay + by + cy;
fz = az;
fw = 1.0;

到目前为止，我们已经通过两次矩阵乘以向量的方法得到了 F 点，那我们说好的矩阵乘以矩阵呢？

上面的点 F 还可以这么理解：

F = cm * bm * A;

设 cm*bm 的结果为矩阵 dm(行主序)，

参照 dm 中元素的索引位置：

[
    0, 1, 2,  3,
    4, 5, 6,  7,
    8, 9, 10, 11,
    12,13,14, 15
]

则 dm 中的第一行元素为：

dm[0] = (1.0, 0.0, 0.0, bx) * (1.0, 0.0, 0.0, 0.0) = 1.0;
dm[1] = (1.0, 0.0, 0.0, bx) * (0.0, 1.0, 0.0, 0.0) = 0.0;
dm[2] = (1.0, 0.0, 0.0, bx) * (0.0, 0.0, 1.0, 0.0) = 0.0;
dm[3] = (1.0, 0.0, 0.0, bx) * (cx, cy, 0.0, 1.0) = cx + bx;

通过 dm 矩阵的第一行元素我们就可以得到点 F 的 fx 值了，我们验证一下：

fx = (1.0, 0.0, 0.0, cx + bx) * (ax, ay, az, 1.0) = ax + cx + bx;

这和我们之前两次矩阵乘以向量得到的结果是一样的。

接下来咱们在把矩阵 dm 的第二行元素写一下：

dm[4] = (0.0, 1.0, 0.0, by) * (1.0, 0.0, 0.0, 0.0) = 0.0;
dm[5] = (0.0, 1.0, 0.0, by) * (0.0, 1.0, 0.0, 0.0) = 1.0;
dm[6] = (0.0, 1.0, 0.0, by) * (0.0, 0.0, 1.0, 0.0) = 0.0;
dm[7] = (0.0, 1.0, 0.0, by) * (cx, cy, 0.0, 1.0) = cy + by;

验证一下：

fy = (0.0, 1.0, 0.0, cy + by) * (ax, ay, az, 1.0) = ay + cy + by;

接下来咱们在把矩阵 dm 的第三行元素写一下：

dm[8] = (0.0, 0.0, 1.0, bz) * (1.0, 0.0, 0.0, 0.0) = 0.0;
dm[9] = (0.0, 0.0, 1.0, bz) * (0.0, 1.0, 0.0, 0.0) = 0.0;
dm[10] = (0.0, 0.0, 1.0, bz) * (0.0, 0.0, 1.0, 0.0) = 1.0;
dm[11] = (0.0, 0.0, 1.0, bz) * (cx, cy, 0.0, 1.0) = bz;

2-先移动后旋转

代码如下：

const mr = new Matrix4();
mr.makeRotationZ(Math.PI / 4);

const mt = new Matrix4();
mt.makeTranslation(0.3, 0, 0);

const matrix = mr.multiply(mt);
const u_Matrix = gl.getUniformLocation(gl.program, "u_Matrix");
gl.uniformMatrix4fv(u_Matrix, false, matrix.elements);

mr 是旋转矩阵

mt 是位移矩阵

mr.multiply(mt) 便是先位移再旋转

效果如下：

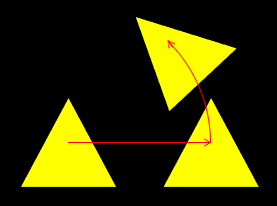
2-先旋转后移动

基于之前的先移动后旋转的代码改一下即可

const mr = new Matrix4();
mr.makeRotationZ(Math.PI / 4);
const mt = new Matrix4();
mt.makeTranslation(0.3, 0.0);

const matrix = mt.multiply(mr);
const u_Matrix = gl.getUniformLocation(gl.program, "u_Matrix");
gl.uniformMatrix4fv(u_Matrix, false, matrix.elements);

效果如下：

3-其它变换方式

3-1-旋转和缩放

• 先旋转后缩放

const mr = new Matrix4();
mr.makeRotationZ(Math.PI / 4);

const ms = new Matrix4();
ms.makeScale(2, 0.5, 1);

const matrix = ms.multiply(mr);
const u_Matrix = gl.getUniformLocation(gl.program, "u_Matrix");
gl.uniformMatrix4fv(u_Matrix, false, matrix.elements);

makeScale() 是矩阵的缩放方法

• 先缩放后旋转

const matrix = mr.multiply(ms);

下图是两种效果的对比：

性质：当缩放因子一致时，旋转和缩放没有先后之分。

如下代码：

const ms = new Matrix4();
ms.makeScale(2, 2, 2);

此是下面的两种变换结果都是一样的:

const matrix=ms.multiply(mr)
const matrix=mr.multiply(ms)

3-2-综合变换

Matrix4 还有一个 compose 综合变换方法，它可以将所有变换信息都写进去，其变换顺序就是先缩放，再旋转，最后位移。

示例代码：

const matrix = new Matrix4();
const pos = new Vector3(0.3, 0, 0);
const rot = new Quaternion();
rot.setFromAxisAngle(new Vector3(0, 0, 1), Math.PI / 4);
const scale = new Vector3(2, 0.5, 1);
matrix.compose(pos, rot, scale);
const u_Matrix = gl.getUniformLocation(gl.program, "u_Matrix");
gl.uniformMatrix4fv(u_Matrix, false, matrix.elements);

compose ( position : Vector3, quaternion : Quaternion, scale : Vector3 )

• position 位置
• quaternion 用四元数存储的旋转数据
• scale 缩放

compose() 方法分解开来，就是这样的：

const mt = new Matrix4();
mt.makeTranslation(0.3, 0, 0);

const mr = new Matrix4();
mr.makeRotationZ(Math.PI / 4);

const ms = new Matrix4();
ms.makeScale(2, 0.5, 1);

const matrix = mt.multiply(mr).multiply(ms);
const u_Matrix = gl.getUniformLocation(gl.program, "u_Matrix");
gl.uniformMatrix4fv(u_Matrix, false, matrix.elements);

第三章 视图矩阵

1-视图矩阵的概念

视图矩阵可以让我们从我们所想要的角度观察物体。

(webgl 画布)中绘图的时候，z 轴数据是没有效果的，因为裁剪空间的 z 轴和 canvas 画布垂直

因此，我们若想看到立体效果，从另一个角度来观察物体。

视图矩阵可以为顶点提供一套新的坐标基底，并获取顶点在这套坐标基底中的点位，然后再将其显示在裁剪空间中。

在高中数学里有一块空间向量的知识，叫做"空间向量分解定理"：

如果三个向量 a、b、c 不共面，那么对空间任一向量 p，存在一个唯一有序实数组(x,y,z)，使

p = xa + yb + zc;

• a,b,c 可以视之为一个三维空间的坐标基底，高中数学里称其为基向量，可构成一个矩阵，一阵便可自成一界。
• x,y,z 可视之为顶点的原始点位。
• 点 p 可理解为顶点的原始点位(x,y,z) 在矩阵[a,b,c]所架构出的新世界的中的点位。

换一个角度观察裁剪空间中的物体，那么基向量还要满足以下条件：

• 基向量需要相互垂直。因为裁剪空间的坐标系是三维直角坐标系。
• 基向量的单位必须是 1，也就是向量 a、b、c 要做归一化，使其长度为 1。因为裁剪空间里三个轴的单位就是 1。

满足了上面的条件后，由矩阵[a,b,c]所架构出的新世界和裁剪空间就只会有旋转方向上的差异，这样新世界里的顶点也可以以另一个角度显示在裁剪空间里。

定义坐标基底 a,b,c

• 视点 e
• 目标点 t
• 上方向 u

2-视图矩阵的布阵思路

1.以视点 e 为终点，目标点 t 为起点，计算向量 d(dx,dy,dz)

d = e - t;

注：向量 d 和视点看向目标的方向正好相反。

2.将 d 归一化

d*=1/|d|

简单说一下归一化思路。

因为：归一化后的向量的长度为 1

所以，我们可以找到向量归一后的长度和向量归一前的长度的比值：

1/|d|

因为：向量的归一化只是改变了向量的长度，未改变向量的方向

所以：归一前的向量和归一后的向量共线且同向

所以：

dx*=1/|d|
dy*=1/|d|
dz*=1/|d|

简写一下就是之前的归一公式：

d*=1/|d|

2.求向量 d 和上方向的垂线 a(ax,ay,az)

a = d ^ u;

空间向量的叉乘

二维向量的叉乘结果可以直接理解为一个实数。

因为二维向量的叉乘是在 x 轴和 y 轴构成的平面里实现的。

其叉乘结果也可以理解为三维空间中 z 轴上的一点。

因为 z 轴上的点的 x,y 值都是 0，可以先不考虑，所以我说二维向量的叉乘结果可以直接理解为一个实数。

严谨来说，两个向量的叉乘结果还是向量。

两个空间向量的叉乘结果必然和这两个向量构成的平面垂直。

其在右手规则下的坐标运算如下:

已知：向量 a(ax,ay,az)，向量 b(bx,by,bz)

求：a^b 的结果 c(cx,cy,cz)

解：

cx = ay * bz - az * by;
cy = az * bx - ax * bz;
cz = ax * by - ay * bx;

3.将向量 a 归一化

a*=1/|a|

4.求向量 d 和向量 a 的垂线 b(bx,by,bz)

b = d ^ a;

5.将向量 d 取反，得向量 c(cx,cy,cz)

c = -d;

上面的方法是为了将新世界的坐标系变成左手坐标系。

基向量 a,b,c 分别对应着左手坐标系里的 x,y,z。

在新世界的左手坐标系里，物体的 z 值越小，视点所看见的就越大。

裁剪空间里的 z 就是下图右手坐标系里的 z。

6.写一个列主序的视图矩阵 matrix

matrix=[
	ax,bx,cx,0,
	ay,by,cy,0,
	az,bz,cz,0,
	0, 0, 0, 1
]

接下来将 matrix 传递给顶点着色器，让其和裁剪空间里的原始点位相乘，便可以从一个新的视角看见裁剪空间里的物体了。

思路已通，接下来我们在代码里手写一个。

3-视图矩阵的代码实现

1.基于视点、目标点、上方向生成视图矩阵的方法

function lookAt(e, t, u) {
  const d = new Vector3().subVectors(e, t);
  d.normalize();
  const a = new Vector3().crossVectors(u, d);
  a.normalize();
  const b = new Vector3().crossVectors(d, a);
  b.normalize();
  const c = new Vector3(-d.x, -d.y, -d.z);
  return [a.x, b.x, c.x, 0, a.y, b.y, c.y, 0, a.z, b.z, c.z, 0, 0, 0, 0, 1];
}

lookAt 方法就是从一个新的角度去看某一个东西的意思

• e 视点
• t 目标点
• u 上方向

在其中我借助了 Three.js 的 Vector3 对象

• subVectors(e, t) 向量 e 减向量 t
• normalize() 向量的归一化
• crossVectors(u, d) 向量 u 和向量 d 的叉乘

2.顶点着色器

<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  //视图矩阵
  uniform mat4 u_ViewMatrix;
  void main(){
    gl_Position = u_ViewMatrix*a_Position;
  }
</script>

3.建立视图矩阵，并传递给顶点着色器

const u_ViewMatrix = gl.getUniformLocation(gl.program, "u_ViewMatrix");
const viewMatrix = lookAt(
  new Vector3(0.2, 0.25, 1),
  new Vector3(0, 0, 0),
  new Vector3(0, 1, 0)
);
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix);

4.绘图方法

gl.clearColor(0.0, 0.0, 0.0, 1.0);
gl.clear(gl.COLOR_BUFFER_BIT);
gl.drawArrays(gl.LINES, 0, indices.length);

效果如下：

4-three.js 里的视图矩阵

lookAt() 方法里，默认视线和上方向不平行。实际开发中，如果视线和上方向平行了，我们需要针对这样的特殊情况做一下处理。

处理方法可参考在 three.js 的 Matrix4 对象的 lookAt() 方法。

const u_ViewMatrix = gl.getUniformLocation(gl.program, "u_ViewMatrix");
const viewMatrix = new Matrix4().lookAt(
  new Vector3(0.5, 0.5, 1),
  new Vector3(0, 0, 0),
  new Vector3(0, 1, 0)
);
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);

第四章 模型矩阵

视图矩阵 -> 模型矩阵

模型矩阵可以对物体进行位移、旋转、缩放变换。

1.在顶点着色器中添加一个模型矩阵

<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  //模型矩阵
  uniform mat4 u_ModelMatrix;
  //视图矩阵
  uniform mat4 u_ViewMatrix;
  void main(){
    gl_Position = u_ViewMatrix*u_ModelMatrix*a_Position;
  }
</script>

2.在 js 中建立模型矩阵，并传递给顶点着色器

const u_ModelMatrix = gl.getUniformLocation(gl.program, "u_ModelMatrix");
const u_ViewMatrix = gl.getUniformLocation(gl.program, "u_ViewMatrix");

const modelMatrix = new Matrix4();
const viewMatrix = new Matrix4().lookAt(
  new Vector3(0, 0.25, 1),
  new Vector3(0, 0, 0),
  new Vector3(0, 1, 0)
);

gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);

3.我们还可以添加一个旋转动画

let angle = 0;
!(function ani() {
  angle += 0.02;
  modelMatrix.makeRotationY(angle);
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);

  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.LINES, 0, indices.length);
  requestAnimationFrame(ani);
})();

3.我们还可以添加一个旋转动画

let angle = 0;
!(function ani() {
  angle += 0.02;
  modelMatrix.makeRotationY(angle);
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);

  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.LINES, 0, indices.length);
  requestAnimationFrame(ani);
})();

4.我们还可以来个弹性动画

let angle = 0;

const minY = -0.7;
const maxY = 0.7;
let y = maxY;
let vy = 0;
const ay = -0.001;
const bounce = 1;

!(function ani() {
  angle += 0.01;
  vy += ay;
  y += vy;
  modelMatrix.makeRotationY(angle);
  modelMatrix.setPosition(0, y, 0);
  if (modelMatrix.elements[13] < minY) {
    y = minY;
    vy *= -bounce;
  }

  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.LINES, 0, indices.length);
  requestAnimationFrame(ani);
})();

扩展-在视图矩阵中释放三角函数的美丽

在视图矩阵中，我们可以将算法和艺术相融合，让它充满乐趣。

就像下面的顶点，就是我通过三角函数来实现的。

风乍起，吹皱一池春水。

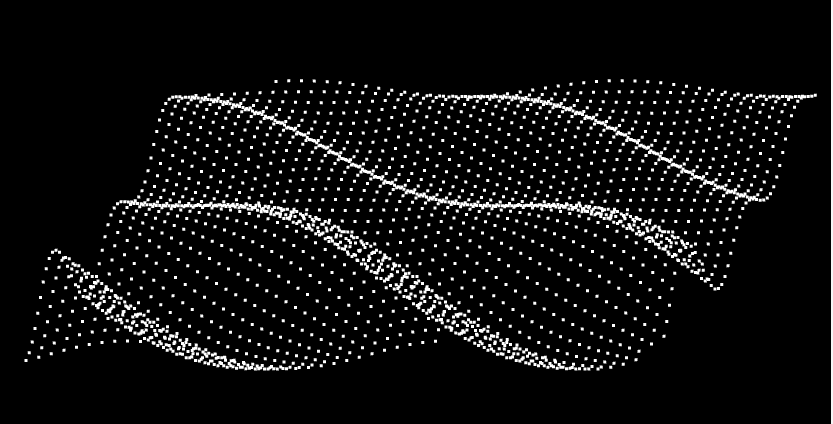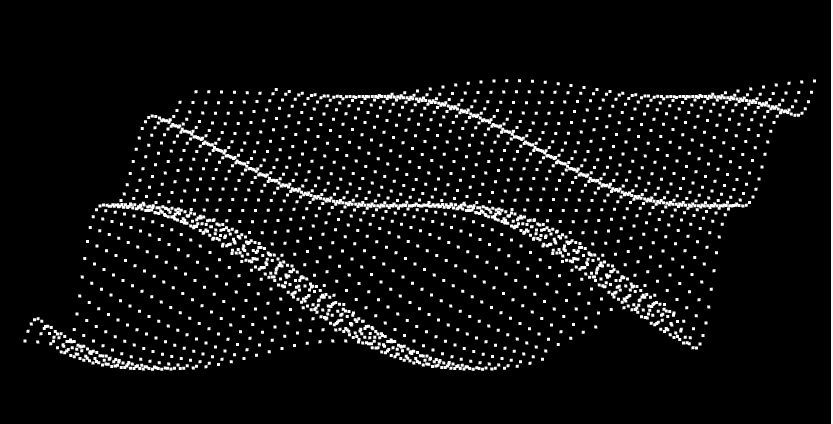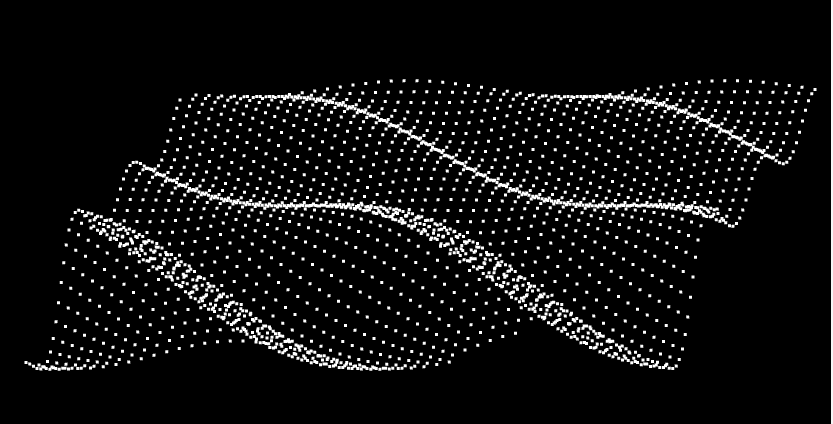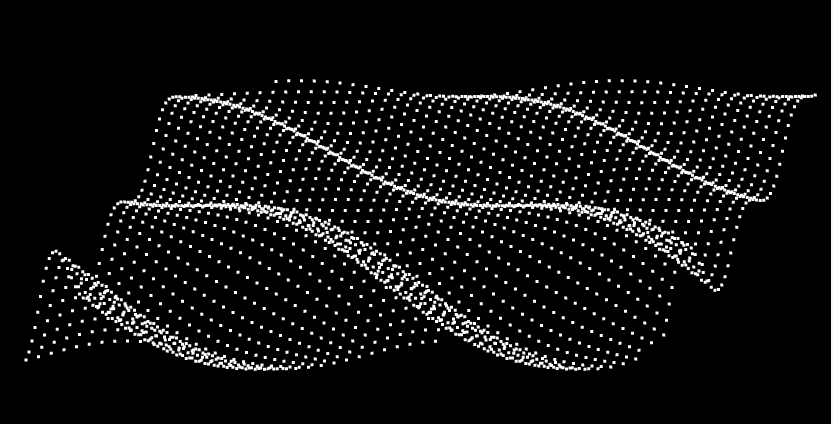
1-正弦型函数

1.正弦型函数公式

y=Asin(ωx+φ)

2.正弦型函数概念分析

已知：

• 圆 O 半径为 A
• 点 P1 在圆 O 上
• ∠xOP1=φ
• 点 P1 围绕 z 轴旋转 t 秒后，旋转到点 P2 的位置
• 点 P1 的旋转速度为 ω/秒

可得：

• 点 P1 旋转的量就是 ω*t

• 点 P2 基于 x 正半轴的弧度就是 ∠xOP2=ω*t+φ

• 点 P1 的转动周期 T=周长/速度=2π/ω

• 点 P1 转动的频率 f=1/T=ω/2π

3.正弦型函数的图像性质 y=Asin(ωx+φ)

• A 影响的是正弦曲线的波动幅度

• φ 影响的是正弦曲线的平移

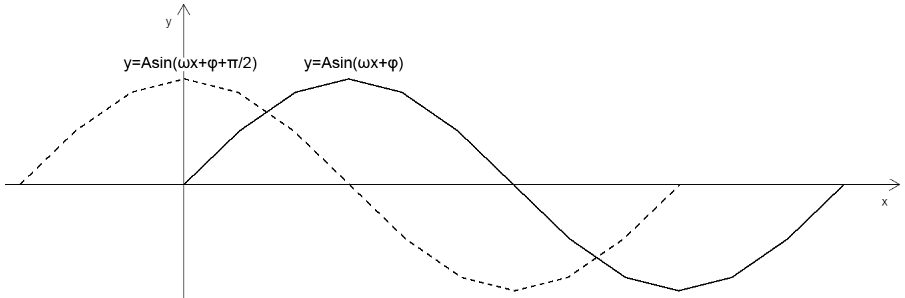
• ω 影响的是正弦曲线的周期，ω 越大，周期越小

通过 A、ω、φ 我们可以实现正弦曲线的波浪衰减。

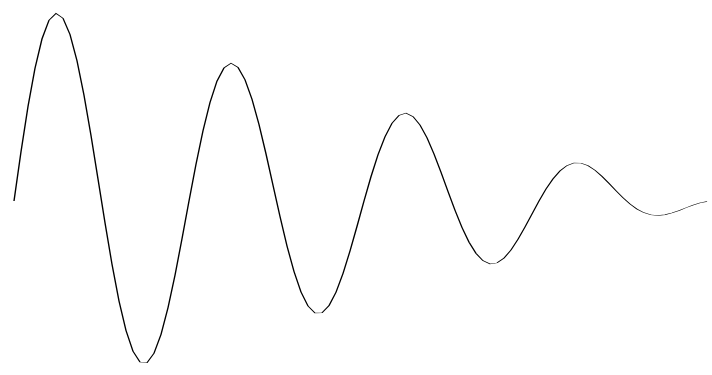
2-代码实现

2-1-布点

1.准备好顶点着色器

<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  uniform mat4 u_ViewMatrix;
  void main(){
    gl_Position = u_ViewMatrix*a_Position;
    gl_PointSize=3.0;
  }
</script>

2.着色器初始化，定义清理画布的底色。

const canvas = document.getElementById("canvas");
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
const gl = canvas.getContext("webgl");

const vsSource = document.getElementById("vertexShader").innerText;
const fsSource = document.getElementById("fragmentShader").innerText;
initShaders(gl, vsSource, fsSource);
gl.clearColor(0.0, 0.0, 0.0, 1.0);

3.建立视图矩阵

/* 视图矩阵 */
const viewMatrix = new Matrix4().lookAt(
  new Vector3(0.2, 0.3, 1),
  new Vector3(),
  new Vector3(0, 1, 0)
);

4.建立波浪对象

const wave = new Poly({
  gl,
  vertices: crtVertices(),
  uniforms: {
    u_ViewMatrix: {
      type: "uniformMatrix4fv",
      value: viewMatrix.elements,
    },
  },
});

Poly 对象，我在之前"绘制三角形" 里说过，我这里又对其做了下调整，为其添加了 uniforms 属性，用于获取和修改 uniform 变量。

updateUniform() {
    const {gl,uniforms}=this
    for (let [key, val] of Object.entries(uniforms)) {
        const { type, value } = val
        const u = gl.getUniformLocation(gl.program, key)
        if (type.includes('Matrix')) {
            gl[type](u,false,value)
        } else {
            gl[type](u,value)
        }
    }
}

crtVertices() 建立顶点集合

/* 建立顶点集合 */
function crtVertices(offset = 0) {
  const vertices = [];
  for (let z = minPosZ; z < maxPosZ; z += 0.04) {
    for (let x = minPosX; x < maxPosX; x += 0.03) {
      vertices.push(x, 0, z);
    }
  }
  return vertices;
}

5.渲染

gl.clear(gl.COLOR_BUFFER_BIT);
wave.draw();

效果如下：

2-2-塑形

1.建立比例尺，将空间坐标和弧度相映射

/* x,z 方向的空间坐标极值 */
const [minPosX, maxPosX, minPosZ, maxPosZ] = [-0.7, 0.8, -1, 1];
/* x,z 方向的弧度极值 */
const [minAngX, maxAngX, minAngZ, maxAngZ] = [0, Math.PI * 4, 0, Math.PI * 2];

/* 比例尺：将空间坐标和弧度相映射 */
const scalerX = ScaleLinear(minPosX, minAngX, maxPosX, maxAngX);
const scalerZ = ScaleLinear(minPosZ, minAngZ, maxPosZ, maxAngZ);

2.建立正弦型函数

function SinFn(a, Omega, phi) {
  return function(x) {
    return a * Math.sin(Omega * x + phi);
  };
}

SinFn 中的参数与正弦型函数公式相对应：

y=Asin(ωx+φ)

• y-顶点高度 y
• A-a
• ω-Omega
• φ-phi

3.更新顶点高度

基于顶点的 x,z 获取两个方向的弧度

将 z 方向的弧度作为正弦函数的参数

a, Omega, phi 先写死

function updateVertices(offset = 0) {
  const { vertices } = wave;
  for (let i = 0; i < vertices.length; i += 3) {
    const [posX, posZ] = [vertices[i], vertices[i + 2]];
    const angZ = scalerZ(posZ);
    const Omega = 2;
    const a = 0.05;
    const phi = 0;
    vertices[i + 1] = SinFn(a, Omega, phi)(angZ);
  }
}

效果如下：


4.修改 updateVertices()方法中的 phi 值，使其随顶点的 x 位置变化

const phi = scalerX(posX);

• scalerX() 通过 x 轴上的空间坐标取弧度

效果如下：


5.修改修改 updateVertices()方法中的 a 值，使其随顶点的 z 向弧度变化

const a = Math.sin(angZ) * 0.1 + 0.03;

效果如下：


2-3-风起

接下来我们可以基于正弦型函数的 φ 值，来一场动画，让它吹皱一池春水。

1.给 updateVertices() 方法一个偏移值，让 phi 加上此值

function updateVertices(offset = 0) {
  const { vertices } = wave;
  for (let i = 0; i < vertices.length; i += 3) {
    const [posX, posZ] = [vertices[i], vertices[i + 2]];
    const angZ = scalerZ(posZ);
    const Omega = 2;
    const a = Math.sin(angZ) * 0.1 + 0.03;
    const phi = scalerX(posX) + offset;
    vertices[i + 1] = SinFn(a, Omega, phi)(angZ);
  }
}

2.动画

let offset = 0;
!(function ani() {
  offset += 0.08;
  updateVertices(offset);
  wave.updateBuffer();
  gl.clear(gl.COLOR_BUFFER_BIT);
  wave.draw();
  requestAnimationFrame(ani);
})();

效果如下：